We are at the finale of the Math Symbols and Their meanings series and we decide to leave the simplest symbols at the end. In this article, you will discover the secrets of mathematical brackets. Do they have any special meanings? Do brackets count in solving a problem? 

Brackets of Mathematics

“( )”

This symbol represents the round parentheses, the most common symbol in mathematics and the simplest. It indicates that whatever is inside the round brackets must be resolved first, overriding the multiplication’s priority. Without the brackets, the operations follow a different order and will give you a different answer. 

Example: (150 – 30) x (6 + 8)

Solution: First, we solve the left bracket (150 – 30), then the second bracket (6+8) and only then we multiply the result of the first bracket with the result of the second bracket.

120  x   14 = 1.680 

Without brackets: 150 – 30 x 6 + 8, first we solve the multiplication 30 x 6, then the subtraction (left to right order) and then the addition. 150 – 180 + 8 =  – 30 + 8 = ﹣ 22.

“[ ]”

This symbol represents square brackets or box brackets. They are used to signal complex operations and to indicate half-open or closed intervals. They also change the order of operations. Treat square brackets as the updated version of round parentheses, because in an equation, whatever is inside the square brackets is going to be solved first. 

Example: [(1+4) x (8 – 6) + 3] x 3 = [(5) x (2) + 3 ] x 3 

      = [10 + 3] x 3

      = 13 x 3

      = 39

“ { } ”

Called “curly brackets” or “braces”, these brackets are used in sets. 

Example: {1, 2, 3, 4, 5, …, 10}

“ ⟨  ⟩ “

These brackets are used in quantum mechanics and are known as the “angle brackets”. They are also used in linear algebra indicating an inner product such as the scalar or dot product.

Example: ⟨𝐮,𝐯⟩= u1v1 + u2v2 + u3v3

Now that you are familiar with the fundamentals of mathematical symbols, it’s important to remember the order of operations. When you don’t respect the order of operations, you will obtain the wrong result. 
Order of Operations

1. First, we solve all the operations within the parentheses ( ) and brackets [ ], { };
   
   
2. Then we solve all the multiplication and division operations;
   
   
3. Lastly, we solve the addition and subtraction operations in order from left to right. 

Basic Algebra Formulas With Brackets

These basic formulas are known as fixed identities which means that the solving process follows the same pattern in all situations:

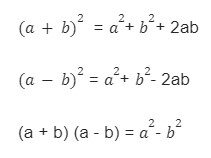
What happens when we substitute power 2 with another number? 

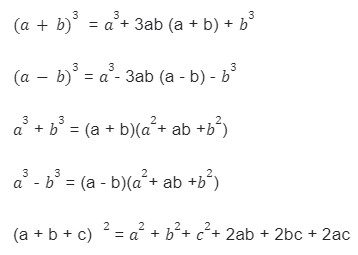
When you see two parentheses or two numbers stuck to each other but there is no operation symbol, please remember that the operation symbol is “x”, multiplication. Thus, the following expression “2ab”, actually means: 2 x a x b. 

Let’s Practice

Our 10 – parts Math Symbols and Their Meanings series is at the end but mathematics is an infinite challenge. What better way to finish a mathematical series than with practice!

Solve the following problems: 

1. (6 – 3) x 8 = ? 
   
   
2. 6 + 3 x 2 + 7 = ? 
   
   
3. (8 + 4) ÷ 3 x 6 = ? 
   
   
4. 5 x (12 – 5) + 7 = ?
   
   
5. (3 + (5 x 4)) – ((4 x 6) – 10) = ?
   
   
6. (5 – 3)2 = ?
   
   
7. Which expression equals 72?
   a)   36 ÷ 4 – 3 x 2 
   b)  (36 ÷ 4 – 3) x 2 
   c)   36 ÷ (4 – 3 x 2) 
   d)   36 ÷ (4 – 3) x 2
   
   
8. In the following expression, what operation would you do first? 4 x [(15 – 6) x (7 – 3)]:
   a) multiplication 
   b) addition 
   c) subtraction
9. Which expressions equal 8?
   a) {5+[6-(3 x 2)] -1}
   b) {[5 + (6 – 3) x 2] – 1}
   c) {5+ 6 – [3 x (2 – 1)]}
   
   
10. Expand the following algebraic identities expressions:
    a) (3x − 2) (3x + 2)
    b) (5d – 6)2
    c) (34+2) 2
    d) (x + y + 4)3

Challenge your classmates to solve the above exercises, or, if you are a parent try to solve them in parallel with your child as a family activity.

Follow our blog for more activities that can help mathematicians feel welcomed in the family.

If you are still unsure about some particular math symbols and how to use them contact our OMC math tutors.

Dive right into the mathematical universe by joining the OMC programs for middle and high school students where we offer group lessons or individual tutoring, tailored for the comprehensive level of each student.