For high school math students, algebra is one of the most intimidating topics in the entire math curriculum. It is a subject that covers a wide variety of subtopics and introduces students to new ways to solve particular math problems.

To give you an idea of just how much subject matter high school math students must cover in algebra, just take a look at this curriculum. More than enough topics to cause a headache! 

As if that wasn’t enough, some algebraic issues, like quadratic equations, need to be solved with a complicated calculator that high school students likely haven’t dealt with before. 

Luckily for those students, – and their guardians – Online Math Center is here to show you how you can solve any quadratic equation, without needing that convoluted calculator.

What Are Quadratic Equations?

There are many uses for quadratic equations, and they have a multitude of useful applications in astronomy, engineering, and physics. Basically, we use quadratic equations to create graphs of functions. For example, when we launch a rocket into space, the path the rocket takes is described by a quadratic equation.

The word “Quadratic” comes from the word “Quad” which means square. This is what tells us that some part of the equation will be “squared”, that is to say, to the power of two. This tells us that we will be solving for x, and that there are a maximum of two answers for x.

The standard form of a quadratic equation is the following:

ax2 + bx + c = 0.

Looking at the equation, we see that it is a second-degree equation in x. For these equations, x is the variable, and a, b, are the coefficients, and c is what we call the constant.

Coefficients can help us immediately identify if an equation is quadratic or not because the first condition for an equation to be a quadratic equation is that the coefficient of x2 is a non-zero term(a ≠ 0). 

This may all sound quite new, and that’s ok. For now, the most important thing to remember is that we are solving for x, and that x will have a maximum of two values.

Finding The Roots Of A Quadratic Equation

When high school math students solve for x, what they are really doing is identifying the roots of the equation. Sometimes, this is quite an easy task, whereas, other times, we need to use a special formula to find the roots of the equation. 

Let’s look at a simple example together:

x2 – 3x – 4 = 0 

With problems like this, we can quickly factorize to find the roots, as follows:

x2 – 3x – 4 = 0

(x – 4)(x + 1) = 0

x – 4 = 0 , x + 1 = 0

x = 4 , x = -1

Now, we have our two roots. Let’s pop each of them back into our equation, to confirm they are correct. 

At x = -1, (-1)2 – 3(-1) – 4 = 1 + 3 – 4 = 0

At x = 4, (4)2 – 3(4) – 4 = 16 – 12 – 4 = 0

Here, we have confirmed that our answers are correct, by putting the roots back into the equation. If our answers here did not equal zero, it would be clear that we have made an error earlier on in the process. 

This means that, since our roots are x = -1, and x = 4, our graphed function will cross the x axis at x = -1 and x = 4.

This is the way we solve straightforward quadratic equations, but how do we tackle more complex ones? 

The Quadratic Formula 

Unfortunately for high school math students, not every quadratic equation’s roots can be found as easily as the problem laid out above. When we are faced with more difficult tasks to tackle, there is a special formula we can use to find the roots of these more complex equations: 

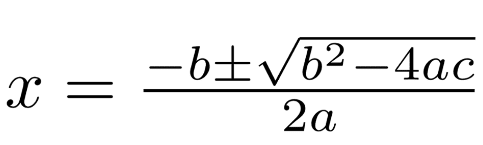
Now, this equation might look absolutely terrifying, at first glance, but we are actually already familiar with most of its elements.

We know that a and b are coefficients, we know that c is the constant and we know that we are solving for x. We even know that there will be a maximum of two solutions for x, hence the ± symbol after the ‘-b’. This symbol makes it clear that the solution(s) can be real or complex.

As you can see, quadratic equations are not always so straightforward, but neither are they as scary as they may have seemed at the start of this article. 

Stay tuned to this page for upcoming pieces, where we will be diving further into the quadratic formula, as well as sharing some helpful hints and tips to help high school math students shine when solving quadratic equations.

High School Math Courses At Online Math Center

Quadratic equations are just the tip of the algebra iceberg that all high school math students are heading towards. Make sure your young learner is thriving, as opposed to just surviving, in math class. 

Enroll them in a high school math course right here at the Online Math Center, to ensure they stay ahead of the curve.