We have previously presented the linear functions, part of SAT math competitions that all students should know how to solve. Another function or equation that students will stumble upon on the SAT math tests is the quadratic function.
We have previously presented the linear functions, part of SAT math competitions that all students should know how to solve. Another function or equation that students will stumble upon on the SAT math tests is the quadratic function.
What is a quadratic function?
While linear functions are indicated on a graph by a straight line, quadratic functions result in coordinates of a parabola (a curved line that opens upside, or downside). Please remember that any graph that intersects with the vertical line more than once cannot be a function.
Characteristics of a quadratic function
Quadratic functions have several characteristics that help mathematicians identify them right away.
- The output variable is always squared
- The shape of a quadratic function is a parabola
- The y-intercept is indicated by (0, y) being the starting point
- The x-intercept, point of zero value, indicated by (x, 0)
- The point at which the parabola cuts the x-axis is known as the x-intercept
- The point at which the parabola cuts the y-axis is known as the y-intercept
- The vertex is the maximum or minimum value of the parabola
- Symmetric points reflect the values of other points on the graph, thus known as mirror points.
The formulas of a quadratic function
The standard form of a quadratic function is: y = ax2 + bx + c , with the highest degree being 2.
The intercept form is indicated by the following formula y = 2 (x + 3) (x – 1).
The vertex form of a quadratic function is indicated by: y = a(x-h)2+ k, where h and k are the vertex value ( h is the coordinate point on x-axis, while k is the coordinate point on y-axis);
The x value of the vortex can be achieved by using the following formula: x = -b2a
How to solve quadratic equations
Factoring
Given the following equation: x2 + 5x -6 = 0, we split it into binomials, and rewrite it as (x + 6)(x – 1) = 0, because 6 multiplied by – 1 = – 6, and 6 + (-1) = 5.
At this point, things get easier because:
(x + 6) = 0, x = – 6
(x – 1) = 0, x = 1 , so the solution to the x2 + 5x -6 = 0 is x = (- 6, 1)
Star method
This is a more difficult method, however, a quadratic equation led by a coefficient is rarely tested during SATs.
We have the following quadratic equation, led by a coefficient:
8x2 + 2x – 3 = 0.
It is called the star method, because in order to facilitate the solving process, we have to draw a star-like graph, and assign the standard form’s values y = ax2 + bx + c, in the following manner: a and c in the upper part of the star, y and b in the lower part of the star.
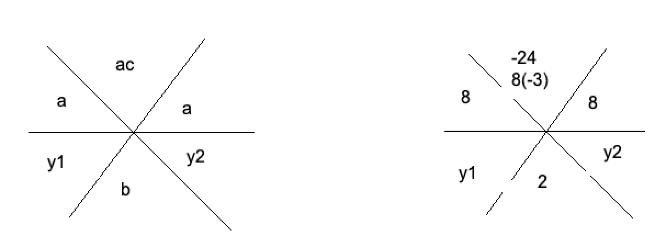
The next step is to find y1 and y2, such that: (y1) (y2) = ac, and y1+y2 = b, therefore:
(y1) (y2) = – 24
y1 + y2 = 2, thus y1 = -4 , and y2 = 6
Now, we substitute the values in the Star method, and we will obtain two fractions:
8-4 and 86 , and by reducing them we obtain: a = 2 , 4 , y1 = -1, and y2 = – 3.
Thus, the final formula would be:
(2x – 1) (4x + 3) = 0, and the solution: x = 12 , -34
Completing the square
We have the equation: x2 – 6x + 8 = 0.
The next step is to move 8 on the other side, resulting in x2 – 6x = – 8, we take 6 and square it on both sides as it follows:
x2 – 6x + 32 = – 8 + 32 in order to achieve symmetry (whatever we operate in the first equation, we need to operate in the second equation, as well)
We simplify the equations in order to obtain a complete square, thus:
x2 – 6x + 9 = – 8 + 9, so it is perfectly factorable. Further on, we will have:
(x-3)2 = 1
(x – 3) 2 = 1 , in order to extract the square.
X – 3 = -1 and x – 3 = 1, we solve the two independently.
X – 3 + 3 = – 1 + 3, x = 2
x – 3 = 1 = x -3 + 3 = 1 + 3, x = 4
Quadratic formula
We have the given equation 2x2 – 4x – 16 = 0,
x = -b b2 – 4ac2a , a formula that you have to memorize in order to solve the equation with it.
In our case, x = 4 (-4)2 – 4(2)(-16)2(2) = 4 1444 = 4 124 = 4 , -2
Still not ready for SAT?
At the Online Math Center, our math tutors offer individual training for SAT competitions. Our goal is for the student to understand the logic behind the solution, and thus, be able to solve independently unknown problems. Get a higher score at SAT by reaching out to us! Let’s get started!