SAT math tests are a system of mathematical tests in four sections such as numbers and operations, functions, geometry and measurement, statistics, and probability. These tests look to determine what the student learns throughout the schooling years, and what sort of skills they require in order to succeed after graduation.
Linear Equations are a fundamental type of exercise that students will have to solve during SAT tests. Let’s take a look at what linear equations are, and how to solve them.
Linear equations
The definition of a linear equation is actually in the name. “Linear” indicates that the equation will be represented in the Euclidean plane as a straight line, and the “equation” indicates that the value is given by a formula.
Linear equations can be represented by the following operations:
y = 2x
y = x + 3
y + 3 = –34( x – 4)
The most common characteristics of a linear equation are:
- It is an equation in which the highest power of the variable is always 1;
- Also known as a one-degree equation;
- The graph of a linear equation will always form a straight line;
- It has only one or two variables;
The critical values of linear equations:
- Slope: it is the point given by the rise over run lines, thus a slope is: riserun , it shows the rate of change.
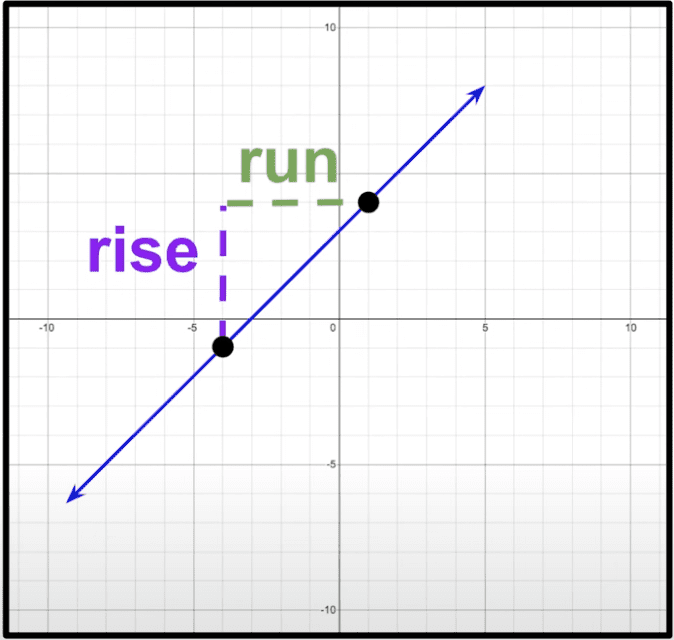
- The Y- intercept is the starting point, represented on the y-axis and indicated by (0, y)
- The X-intercept is the point of zero value at which the equation intersects the x-axis, indicated by (x, 0)
Forms of Linear Equations
Below are the most common forms of linear equations tested during the SAT.
Slope-intercept form
Given by the equation, y = mx + b, where m is the slope, b is the y-intercept;
Point-slope form
Indicated by the equation, y – y1 = m(x – x1) , where m is the slope, and the (x1, y1) is any coordinate of any point on the line.
Standard form
It is written in the form of Ax + By = C, where A, B, and C must be integers and A must be positive.
How to solve systems of Linear Equations
In SAT tests, you will stumble upon problems of two lines and where they intersect, the intersection representing the system of the linear equations. There are two ways in which to solve systems of linear equations.
Through substitution
In the case of isolated y, the solution is simple. It only requires the substitution of one of the y’s in the equation of the other y. Given the following equations:
y = 2x+1 and y = –23x-7 , we can substitute by writing 2x + 1 = – 23x – 7, then we solve the equation and identify x. The next step is to substitute the “x” in each equation with the calculated value and find out the value of y. In this case, y = – 5, can you test to see if you reach the same result?
Through elimination
Elimination can be simpler than substitution, but not necessarily the all-cases solution. Compared to substitution, in case of elimination, we match up the equations and then we add them together so one of the variables is cancelled out.
Given the two equations:
y = 2x+1
y = –23x-7, in order to be able to add them up, we need to get rid of the fraction in the second equation, so we multiply it with 3, and the resulted equation will be:
3y = -2x – 21, we add this equation to y = 2x + 1, so we can cancel -2x with 2x, and obtain 0. So we will have 3 y + y = 4y, and – 21 + 1 = 0, ending up with the equation: 4y = – 20, which will take us to the result of y = – 5.
Are you training for SAT?
At the Online Math Center, our math tutors teach extensive SAT math so our students obtain high scores. Reach out to us for SAT tutoring, or simply to upgrade your math skills with our individual tutoring programs.