By the time students reach 7th grade, they know their math lessons and private math tutoring classes often challenge their minds in ways other school subjects do not. Math has a certain way of opening our minds to new ways of thinking, interesting concepts, and fascinating processes to find solutions.
One particular topic that perplexes students year in and year out is the special cases of the sum of a cube and the difference of a cube. These special cases when multiplying polynomial expressions can seem extremely complicated at first sight, especially for students that struggle with polynomial expressions and other topics in algebra.
Once students learn the necessary skills to tackle these seemingly confusing problems, the ability to do so becomes a valuable tool for solving algebraic equations. The right school teachers and individual tutors can demystify these challenging concepts and pave the way for academic success.
Sum of Two Cubes
Let’s start with the sum of cubes. Put simply, the sum of two cubes is the answer when we find the cube of any binomial in the form (a + b)³, where ‘a’ and ‘b’ represent any two real numbers.
We can expand this into a formula that is easier for us to break down, manage, and solve
(a + b)³ = a³ + 3a²b + 3ab² + b³
Understanding this formula allows us to simplify complex algebraic expressions and solve equations much more efficiently. We must be able to recognize these kinds of patterns and use them to our advantage when we are faced with similar problems.
Difference of Two Cubes
Now that we’ve looked at the sum of two cubes, and expanded on the formula, let’s dive into the difference of two cubes. This concept, similar to the sum of two cubes, involves finding the cube of a binomial. This time, however, we will be working with subtraction instead of the division we saw in the previous example.
Like the sum of two cubes, when we express the difference between cubes, ‘a’ and ‘b’ are any two real numbers. The expression is written like this: (a – b)³.
And, similar to the sum of two cubes, we can expand the expression to read:
(a – b)³ = a³ – 3a²b + 3ab² – b³
The difference of cubes formula is an invaluable tool that will help students to factor expressions and analyze the behavior of functions quicker and more efficiently.
Geometric Example
Let’s take a look at an example from geometry, courtesy of our friends at Math is Fun.
There are two cubes, one of lengths x and the other of lengths y:
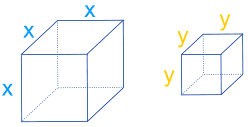
We can split the larger “x” cube into four small cuboids, with box A being a cube with sides the same length as “y”:
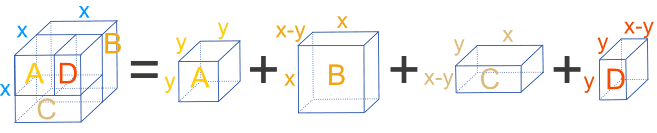
We can write the volumes of these boxes as follows:
A = y3
B = x2(x − y)
C = xy(x − y)
D = y2(x − y)
We know, however, that these four boxes, A, B, C, and D make up the larger cube which has a volume of x3.
Therefore, we can say:
x3 = y3 + x2(x − y) + xy(x − y) + y2(x − y)
x3 − y3 = x2(x − y) + xy(x − y) + y2(x − y)
x3 − y3 = (x − y)(x2 + xy + y2)
x3 − y3 = x3 – 3x2y + 3xy2 – y3
Factoring the Sum and Difference of Cubes
I’m sure by now that you’re fully understanding the sum of cubes, the difference of cubes, and the ways you can solve such problems quickly. Factoring the sum and difference of cubes can be tough, even after seeing the process done in an example. In fact, factoring high-degree polynomial expressions is a tricky task for anyone.
To make math even more challenging, some students are visual learners and can benefit more from a video than several written examples. If that’s you – or your young one – be sure to take a look at these great explainer videos to see how you can factor higher-degree polynomials, and specifically how to factor the difference of cubes and the sum of cubes.
At Online Math Center
Our tutors have decades of combined experience dealing with every math problem under the sun, from polynomial expressions like these to trigonometric head-scratchers and everything in between. We offer personalized, individual tutoring classes to children of all ages and abilities, because we know that classes focused on plugging one child’s learning gaps are more valuable than dozens of classes shared with twenty other students.
We also offer tailored SAT preparation classes, intensive preparation classes for math competitions, and individual tutoring sessions for middle school students, and high school students. Our results speak for themselves, with over 500 students improving their math grades after taking classes at OMC.
Contact OMC today and help your child make it onto our list of students that have seen their math skills soar after the right tutoring.