As they work their way through their 7th-grade math classes, students will regularly encounter new concepts, principles, and expressions. Sometimes, children are already familiar with something, they just don’t know its name, or they know it by a different name.

One such term is monomial, a polynomial expression with just one term. Well, then, what are polynomial expressions, I hear you ask?

Polynomial expressions are mathematical expressions with more than one term. The name comes from Greek, with poly- meaning “many” and -nomial meaning term, in this case. That gives us “many terms”.

Here is an example of a simple polynomial expression:

Now, we understand the term monomial a little bit better. It is a polynomial expression with just one term. Here are some examples of monomials:

Polynomials can have constants (represented above by the c), variables (x), and exponents (the 4 in y⁴). Here is an example of a polynomial expression:

In this example, the constant is 9, the exponent is 2, and x is our variable. 

Addition And Subtraction Of Polynomial Expressions 

Now that we’ve established what polynomial expressions are, as well as monomials, we can begin learning how to add polynomial expressions together and subtract one polynomial expression from another.

Adding polynomial expressions is easy, we simply add the like terms together. Like terms are terms that share variables. For example: 8x, -4x, and x are all like terms, because all the variables are x, all that changes in these expressions are their coefficients (the number you multiply your variable by, such as 8, 4, and 1 in the above examples).

Let’s try an example. We want to add

We simply split the expressions into their like terms, and add them separately:

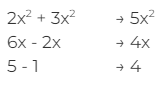
Now, we combine the individual terms to get our resulting polynomial expression. Our answer is:

Next, we need to look at how to subtract polynomial expressions. Thankfully, it is not too much more complicated than adding polynomial expressions. The important thing to remember is that we must reverse the sign of each term that we are subtracting. After switching all the positive terms into negative terms, and vice versa, we can simply add the terms as above.

Let’s try it out using some new examples. 

Our equation now reads

First, we must reverse the sign of the terms we are subtracting:

Now, we simply add our like terms in our expressions together, as above:

Therefore, our answer is: x2 + 1

Multiplying Polynomial Expressions 

Next up on our journey to fully understand polynomial expressions is learning about multiplying polynomial expressions. The first thing we need to do for this is to understand that there are different ways to multiply polynomial expressions, and which approach we take is determined by the type of expressions we are dealing with.

We take different approaches to multiplying polynomial expressions if the two expressions are monomials, if there is one monomial and one binomial, or if we are dealing with two binomials.

To multiply a monomial by another monomial, we must first multiply the constants, then multiply each variable, and then combine the results to get our answers. Here’s an example:

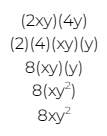
Time to take a look at how we multiply a monomial by a binomial, using another example. To do this, we multiply the single term in the monomial by each of the two terms in the binomial:

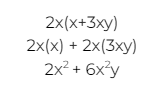
Finally, we have to check out the process for multiplying one binomial by another binomial. For these equations, we will need to perform four different multiplications. This is because we are going to multiply each of the terms in the first binomial by each of the terms in the other binomial. 

Here’s a general example to help you see how it works:

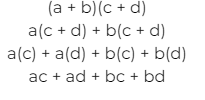
And there they are, the different methods of multiplication we can use to multiply polynomial expressions!

OMC 7th Grade Math Courses 

Make sure your child is able to handle polynomial expressions when they run into them this school year. At OMC, we offer 7th Grade Math Courses, as well as individual tutoring and preparation for test environments. Our team of dedicated professionals boasts decades of experience and can tailor classes depending on the gaps in any individual child’s knowledge.

Contact OMC today to give your young math student the best chance of reaching their potential.