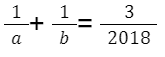Math competitions can be a fuel for evaluation anxiety, but a way to subdue that anxiety is understanding the structure of the exam. Most competitions include both algebra and geometry problems, so checking out past exams will prepare you for tackling the new competition in a more relaxed way.
The Common Structure Of Math Exams

Usually, American math competitions for middle school students comprise 25 questions.
The first 10-15 questions are algebra problems containing probability, counting, fractions, and real numbers, then the final questions refer to elementary geometry including Pythagorean Theorem, spatial visualization, or calculating angles and dimensions.
The lesser questions a math competition has the more challenging is. However, the trick is to always master your grade’s curriculum because competitions are a notch more difficult than school level. If your school doesn’t provide math competition preparation classes, you can check online sources for practicing or math forums where students all over the world discuss solutions to problems.
Type Of Algebraic Exercises
Middle school students can stumble upon problems containing sets of numbers, integers, sums, and fractions. Check out the following exercises that we collected from previous math exams:
- Let S be the smallest set of positive integers such that:
a) 2 is in S,
b) n is in S whenever n 2 is in S,
c) (n + 5) 2 is in S whenever n is in S.Which positive integers are not in S? (The set S is “smallest” in the sense that S is contained in any other such set.)
- Each of the integers from 1 to n is written on a separate card, and then the cards are combined into a deck and shuffled. Three players, A, B, and C, take turns in the order A, B, C, A, . . . choosing one card at random from the deck. (Each card in the deck is equally likely to be chosen.)After a card is chosen, that card and all higher numbered cards are removed from the deck, and the remaining cards are reshuffled before the next turn. Play continues until one of the three players wins the game by drawing the card numbered 1. Show that for each of the three players, there are arbitrarily large values of n for which that player has the highest probability among the three players of winning the game.
- A class with 2N students took a quiz, on which the possible scores were 0, 1, . . . , 10. Each of these scores occurred at least once, and the average score was exactly 7.4.Show that the class can be divided into two groups of N students in such a way that the average score for each group was exactly 7.4.
- Find all ordered pairs (a, b) of positive integers for which:

- Determine all possible values of the expression:
![]()
where A, B, and C are nonnegative integers.
You can check more algebraic problems online on the official website of the AMC or buy math exercises manuals.
Type Of Geometrical Exercises
1. A line in the plane of a triangle T is called an equalizer if it divides T into two regions having equal area and equal perimeter. Find positive integers a > b > c, with a as small as possible, such that there exists a triangle with side lengths a, b, c that has exactly two distinct equalizers.
2. Suppose that A, B, C, and D are distinct points, no three of which lie on a line, in the Euclidean plane. Show that if the squares of the lengths of the line segments AB, AC, AD, BC, BD, and CD are rational numbers, then the quotient:
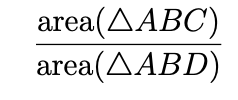
is a real number.
3. Three semicircles have their diameters on the sides of the right triangle ABC. The area of the small semi-circle is 5π and the area of the medium semicircle is 7π. What is the sum of the areas of all three semicircles?
4. A 20-foot ladder rests against a wall so the top of the ladder is 19 feet off the ground. If the top of the ladder drops 6 feet, how far did the bottom of the ladder move?
5. A square and an equilateral triangle have the same perimeter. What is the ratio of the area of the circle circumscribed about the square to the area of the circle circumscribed about the triangle?
Our math Tutors At The OMC...
…are ready to help you get the highest score possible at math competitions.
We offer individual or group tutoring for middle school students that want to acquire better math skills or prepare for future math competitions.
Reach out to us anytime to discuss your math learning goals.