Last time, we discussed the most common geometrical shapes in mathematics. We briefly presented the triangle because it deserves an entire article and you will soon learn the reason.
The triangle is a geometrical figure with 3 sides and 3 angles. The total sum of the three angles is always 180°. In mathematics, there is a special branch dedicated to the study of triangles and it is called trigonometry.
Types of triangles
When we refer to triangles, we categorize them according to the sides of the triangle or the angles.
Triangles according to sides.
Equilateral
An equilateral triangle has all 3 sides of equal length. It is pretty simple to memorize this because the name already indicates this: “equi” meaning “equal” and “lateral” referring to the sidelines. All the angles in an equilateral triangle are 60°.
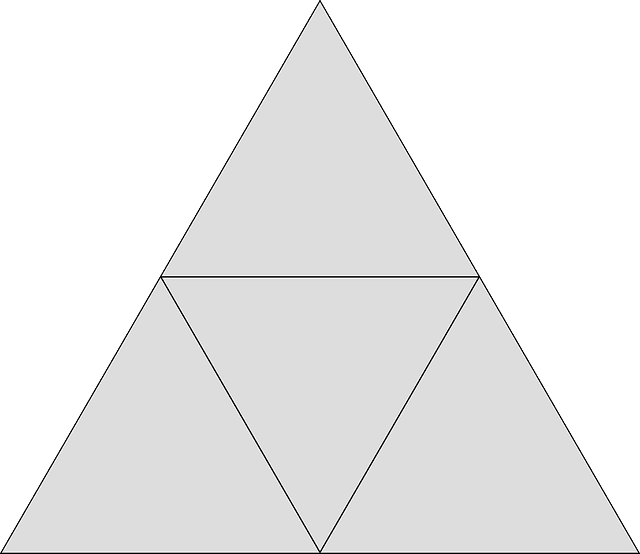
In school, we might be asked to calculate the altitude of an equilateral triangle, its sidelines or the area.
Calculating the measurements of an equilateral triangle:
We use the next formula in order to find out the value of the altitude “h”
h = a sin60°
or
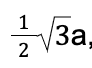
where a represents the sideline.
In order to calculate the area of an equilateral triangle, we use the formula:
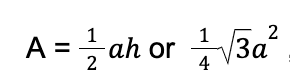
Triangle Theorems: Pythagora, Napoleon, and Morley
The most accessible and known theorem is Pythagoras’.
“In any right-angled triangle, the square of the length of the hypotenuse (the side that lies opposite the right angle) is equal to the sum of the squares of the other two sides.”
Meaning that: a2+ b2= c2 , when one of the angles is 90°.
Theorem of Morley
“The points of intersection of the adjacent angle trisectors of the angles of any triangle △ A B C are the polygon vertices of an equilateral triangle.”
Morley’s theorem is used in complex geometrical problems, but for students interested in spatial geometry, knowing this theorem is a must.
Theorem of Napoleon
“If three equilateral triangles are drawn on the legs of any triangle (either all drawn inwards or outwards) and the centers of these triangles are connected, the result is another equilateral triangle.”
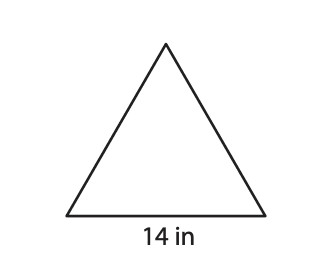
PRACTICE:
Find the area of the following equilateral triangles. Round your answer to two decimal places:
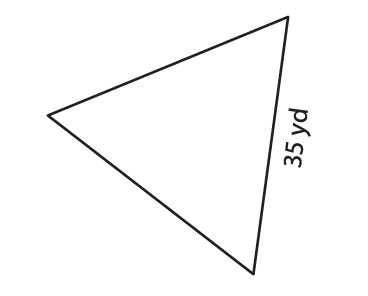
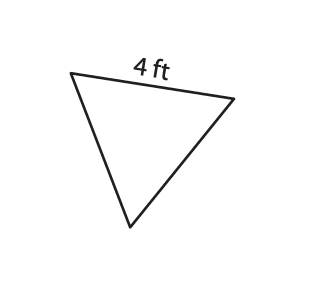
Isosceles
The simple definition of an isosceles triangle is:
An isosceles triangle is a triangle that has at least two sides of equal length.
Structure: When an isosceles triangle has only two congruent sides, we call those sides – legs while the third, unequal side is called the base. The angle opposite the base is called “vertex angle”, and the angles opposite the legs are called “base angles”.
Now that we know the Pythagoras’ Theorem, we can calculate the base, legs, and height by using the following formulas:

In an isosceles triangle, the two base angles have the same value. When the base angles are 45° each, the angle opposite of the base is 90°.
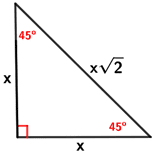
PRACTICE:
The external angle of an isosceles triangle is 87°. Find the interior angles of the triangle.
Scalene
A scalene triangle doesn’t have any equal sidelines. All sidelines in a scalene triangle are unequal.
All angles in a scalene triangle are unequal. There is no line of symmetry and unlike the isosceles and equilateral triangle, if we cut the scalene triangle in two, we cannot obtain two equal halves.
In order to calculate the area of a scalene triangle, we must apply the Heron formula. It’s a two-step formula and it goes like this:
1st step: Calculate the semi-perimeter of the scalene triangle, using the formula:

The perimeter of a scalene triangle is simply calculated by adding the sidelines: a + b + c
A scalene triangle can have acute, right, and obtuse angles.
PRACTICE:
Find the area of the scalene triangle given its three sides: a = 4 cm, b = 5 cm and c = 7 cm.
Triangles according to angles
You might stumble upon exercises that instead of naming the triangles equilateral, isosceles and scalene, they are named after one of the angles. Thus, we have acute, right and obtuse triangles.
Let’s take a look at each of them:
Acute
An acute triangle has all three angles less than 90°. An acute angle can be found in equilateral, isosceles and scalene triangles. Some interesting facts about acute angles are: the sum of angles is 180°, there cannot be a right and acute-angled triangle or an obtuse and acute-angled triangle.
The sideline opposite of the greatest angle is the largest in measurement.
The area of an acute triangle is calculated by:
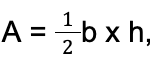
where b is the base and h is the height.
Right
A right triangle is a three-sided polygon with one angle of 90°. The symbol for angles is “α”. Usually, we have a right angle in isosceles and scalene triangles.
Useful formulas
Altitude/ Height of a right triangle:
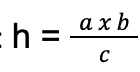
where h is the height, a, b and c are the sidelines.
Area of a right triangle:
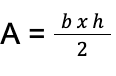
where b is the base and a is the height.
The perimeter of a right triangle: a + b + c
Obtuse
An obtuse-angled triangle has one of the angles greater than 90° (between 90° and 180°). Since the total sum of angles in a triangle must be 180°, it means that in an obtuse triangle, we will have one angle greater than 90°, then the other two angles will be acute.
The area of an obtuse triangle can be calculated by using the common formula:
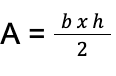
or Heron’s formula. Both can be applied.
Do you want to know more about triangles and how to apply spatial geometry principles? The OMC math tutors offer personalized classes, individually or in groups.
Our math tutoring programs are designed to help middle school students and students that want to participate in math competitions.
Contact us to schedule an appointment and find out more about the OMC math classes.