Before math lessons become complicated, they are simple. Everybody is familiar with the basic geometrical shapes: square, rectangle, and triangle.
These common shapes are with us since infancy in games that develop visual memory and spatial intelligence. Have you ever wondered what is the primal geometrical shape, though?
It All Comes Down To A Certain Point
The point or “dot” or “ ᐧ ” is the geometrical figure that has no length, width, or height. Even so, there are 3 types of points in geometry: the collinear point, the noncollinear point, and the concurrent point.
What Is The Difference Between Points?
A collinear point is any point on a straight line.

Any of the points A, B, or C is collinear point.
Can We Show That Two Or More Points Are Collinear?
We have two methods by which we can prove that two or more points are collinear.
The Slope Formula Method where three points are collinear if the slope of any two pairs of the points is the same.
Application: There are the A, B, C points. We have three-point pairs: AB, BC, AC. If the slope of AB = BC = AC, the three points are collinear.
Exercise: Prove that the following points are collinear: A (2, 4), B (4, 6), and C (6, 8).
Solution: If the three points A (2, 4), B (4, 6), and C (6, 8) are collinear, then the slopes of any two pairs of points will be equal.
Slope of AB/BA = (4 – 2) / (6 – 4) = 2 / 2 = 1
Slope of BC/CB = (6 – 4) / (8 – 6) = 2 / 2 = 1
Slope of AC/CA = (6 – 2) / (8 – 4) = 4 / 4 = 1
Given the fact that all slopes = 1, then A, B, C are collinear points.
The Area of a Triangle Method: If the value of the area of the triangle formed by the three points is zero then the points are collinear. Remember that: A (2, 4), B (4, 6), and C (6, 8), thus A =
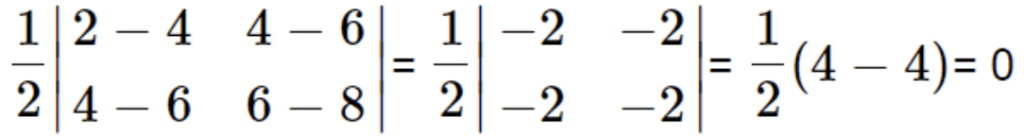
The Noncollinear Points
When two or more points cannot be united by a single straight line, these points are called noncollinear points.
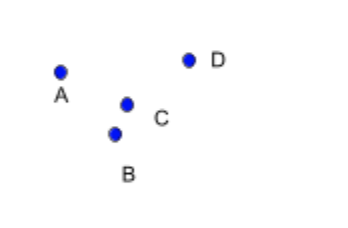
More noncollinear points connected together form regular or irregular polygons.
The Concurrent Points
Any point in which two or more straight lines intersect. Since different types of straight lines can be intersected to form concurrent points, there are different types of concurrent points.
- Centroid point: an intersection point formed by the medians of a triangle. The medians of a triangle are the lines drawn from the middle of a side to the opposite angle.
- Circumcenter point: a concurrent point formed by the intersection of the perpendicular bisectors. A perpendicular bisector is a line that intersects another line at a right angle and divides that line into two equal parts at its middle point.
- Incenter point: a concurrent point inside the largest circle of a triangle and it is formed by the lines that originate at the vertex and extend to the opposite side.
- Orthocenter point– is the point of intersection formed by the three altitudes of a triangle.
Fun Facts Of The Concurrent Points
- When we have a right-angled triangle, the orthocenter is always at the vertex of the right angle.
- When we have a right-angled triangle, the circumcenter is always the midpoint of the hypotenuse.
- The Euler line contains the orthocenter, centroid, and circumcenter for any triangle in all circumstances and the three points are, in fact, collinear as they belong to the same straight line.
- The centroid of a triangle falls between the triangle’s orthocenter and circumcenter, in all cases.
- The distance from the centroid to the circumcenter is always half the distance between the centroid and orthocenter.
- When we have an acute triangle, the circumcenter always falls inside the triangle.
- But when it comes to obtuse triangles, the circumcenter is always outside the triangle and always opposite the obtuse angle, while the orthocenter is also outside the triangle, opposite the longest leg of the triangle.
- All four points of concurrency can themselves be concurrent! However, when it comes to equilateral triangles the centroid, circumcenter, incenter, and orthocenter will always be the same point.
Don’t believe these fun facts? Try to prove these interesting theories by yourself and let us know what you found out!
Also, try to solve the exercises below:
- Show that the following points are collinear or not:
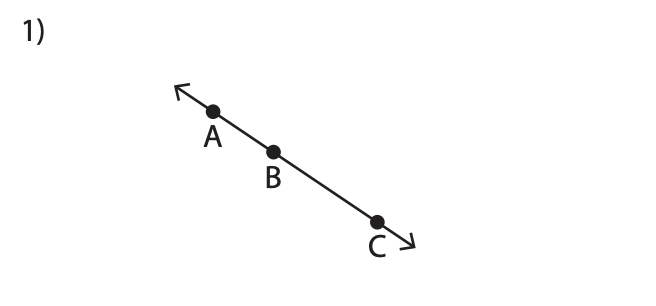
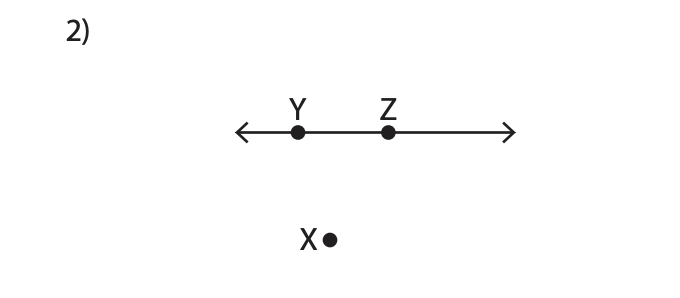
Are the ABC points collinear? Are the XYZ points collinear?
- Write True or False at the end of each sentence:
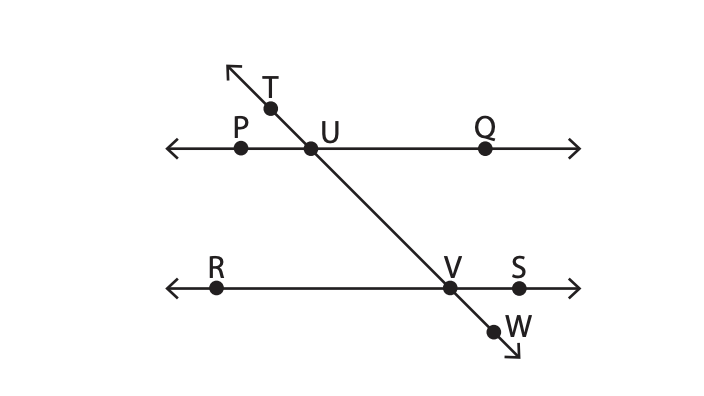
a) Points T, U and V are colli
b) Point U is collinear with the points R and S:
c) Points S, R and Q are not collinear:
d) Points P, R and U are collinear:
e) Point S is not collinear to TW and collinear with the point V:
What We Can Help You With
Are you interested to learn more about geometry?