Middle school math lessons can be places of great discovery for students. By the time children reach eighth grade math class, they will have been introduced to many topics, some more interesting and memorable than others. In my experience teaching math, students often enjoy learning about squares and square roots, especially when we show them what squaring a number really means with a visualization.
By the time eighth grade rolls around, students are expected to be able to handle simple squares, cubes, and square roots, and throughout that year they will learn more about square roots, their properties, and how this topic can help them succeed in math class moving into high school and beyond.
Squares and Cubes
Squares and cubes are mathematical concepts that are used in a variety of fields of study. Reaching far beyond the middle school math classroom, people will use these concepts in their physics, economics, and engineering careers.
In simple terms, a square is a number that is multiplied by itself. 2 squared (written 2²) is 2 x 2, which equals 4. A cube (denoted by a ³) is a number that is multiplied by itself twice. That means that 2 x 2 x 2 = 2³. Therefore 2³ = 2 x 2², which means 2³ = 2(4), and we arrive at the answer 2³ = 8.
Some of our more dedicated readers will know we covered all about squares and cubes in a previous article, so be sure to check that out for a more in-depth look at the basics of squares and cubes.
As a reminder – or an introduction for those of you who haven’t read the previous article yet – let’s look at the visualization example I mentioned earlier. Before we see this image, let’s think about the word “square” for a second. Is there anything about this word, and what it means in literal terms, that might help us better understand the mathematical concept a little bit better?
Let’s imagine our number as individual units, laid out in a line. Now, with that image in mind, what will happen to that line if we multiply it by itself? What happens is that our line becomes a square. When we count up all the individual units that make up this square, we will get a new number, which equals to our original number multiplied by itself (or, squared).
Here is the image that should clarify any doubts:
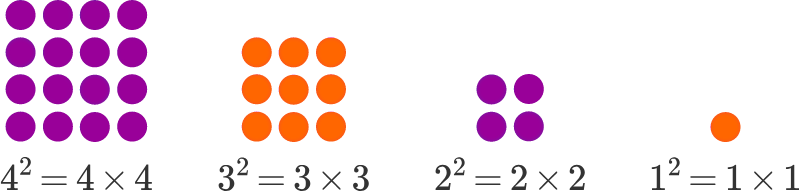
Here we can see how 4² leaves us with 16 units, 3² with 9, 2² with 4, and 1² with just one.
Now that we understand squares more clearly, let’s take a look at square roots, often thought of as the opposite of a square.
Square Roots
Let’s dive right into an example and see this concept in action.
We can say that √4 = 2, because 2 x 2 = 4. Similarly, we can say √9 = 3, as 3 x 3 = 9.
These kinds of squares, cubes, and square root problems will be manageable for most students, but where extra work is often needed outside of the classroom is when students reach grade eight and are introduced to some of the properties of square roots. These concepts can be a little bit more tricky and they are often cited as one of the lessons that require some individual work at home, or with a tutor.
Square Root Properties
There are several properties that apply to all square roots, and we are going to introduce the first three, which are the most important for middle school students. Of course, moving forward in their education, students will be expected to understand and be able to use more and more of these properties in more advanced math, and perhaps science, classes.
The product property
The square root of any product is equal to the product of the square roots of the factors. If we want to put this into an equation, we can say that the product property tells us that √(ab) = √a x √b.
For example, the square root of 12 is equal to the square root of 4 multiplied by the square root of 3. Therefore, we can say √12 = √4 x √3.
The quotient property
Next is the quotient property, which states that the square root of a quotient is equal to the quotient of the square roots of the numerator and denominator.
This property says that √(a/b) = √a / √b.
Looking at an example, we could say the square root of 16/4 is equal to the square root of 16 divided by the square root of 4, or √(16/4) = √16/√4. This will bring us to 4/2 which we know is 2, a.k.a. The square root of 4.
The power property
The final property we will look at is the power property, which tells us that the square root of a number raised to any power is equal to the number raised to half of that same power. Basically, the power property states √(a^n) = a^(n/2).
Let’s choose 25 as our number for this final example. The square root of 25 squared (25²) is equal to 25 raised to half the power, or √(25²) = 25^(2/2) = 25.
After these, students will learn about the conjugate property, the additive property, and many more properties of square roots.
At Online Math Center
When your child needs help thriving in their middle school math class, turn to qualified professionals with years of experience to guide them through the more challenging topics, and plug any gaps they may have in their knowledge.
We provide a full range of individual tutoring services, including classes focused on each grade throughout middle and high school, intensive SAT preparation courses, and math competition preparation courses, as well.
Contact OMC today and enroll your child in our eighth grade math courses, so you can rest easing knowing they are prepared for squares, square roots, and whatever else math class may throw at them.