Circles are quite literally everywhere. That mug on your coffee table is in the shape of a circle. That ring on your finger – circle. The bowl you ate your cereal from? That’s right, circle. The basics of a circle, like how to find the area, circumference, and more are all very applicable information in daily life, and therefore they make for valuable concepts for school children to learn.
Understanding the diameter of a plate for hosting parties, the area of a circle to find the volume in your cup, and the diameter of that birthday cake, are all different instances where you may find it useful to understand the properties of a circle. Engineers use circular measurements to design bicycles, tires, rockets, etc. Architects also use the symmetrical properties of a circle to design buildings, athletic tracks, Ferris wheels, and so much more.
The Basics
The basic properties of circles include the radius, diameter, area, and circumference. Having a strong understanding of these basics is important in order to comprehend more complex properties. We know a circle is a round, two-dimensional shape where all points along it are the same distance (equidistant) from the center.
The radius (r) of a circle is the distance from any point along the circle to the center. The diameter (d) of a circle is the distance from any point along the circle to another point, passing through the center. It must pass through the center in order to be considered the diameter. This is essentially doubling the radius (d = 2r). The circumference (c) of a circle is the distance around the circle’s edge.
We solve for all of these values with simple equations. You can find the circumference of a circle by multiplying the diameter by pi (𝛑 or 3.1415…). If you do not know the diameter but know the radius, you could double the radius and then multiply by pi. On the flip side of that, if we wanted to know the diameter but only had the value of circumference, we could simply divide the circumference by pi. The area (A) of a circle is the space inside and it can be easily calculated using A = 𝛑r².
A = 𝛑r²
C = 𝛑d
d = 2r
d = C𝛑
These four equations listed above are key for all young math students to learn and they will help them massively in getting comfortable with finding the area, circumference, diameter, and radius of a circle. Armed with this knowledge, middle and high school students will be ready to tackle any problems relating to circles that may pop up in math class.
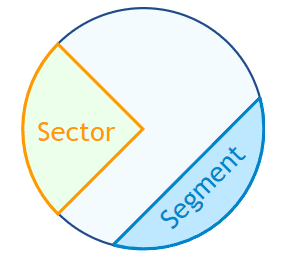
Sectors
A sector of a circle is essentially a “slice” within this round shape. If you think of a slice of pie or pizza, this is what we would call a sector in mathematics. It is two points along the edge of the circle back to the center, creating a “slice”. What is crucial to a sector is the angle that it forms. In any sector, there is an angle which is represented by the symbol θ. The angle can either be measured in radians or degrees. If θ is in radians, the area of a sector can be calculated with the below formula:
θ2𝛑 x 𝛑r²
which can then be simplified to: θ2 x r²
However, if θ is in degrees, the formula must be adjusted to:
θ x 𝛑/360 x r²
Segments
A segment of a circle is the space created by a line from one point along the edge to any other point. The difference between a segment and sector is quite obvious. Rather than a “slice”, a segment is a piece of the circle without an angle formed from the center point.
To solve for the area of a segment, we would still need to understand the angle (θ) which can be either in degrees or radians. Even though there is no actual angle created in the segment, we still need to connect the two points to the center to understand what the angle (θ) is. The property of sine (sin) is also used to solve for the area of a segment.
A = θ – sin(θ)/2 x r² (when θ is in radians)
A = ( θ x 𝛑/360 – sin(θ)/2 ) x r² (when θ is in degrees)
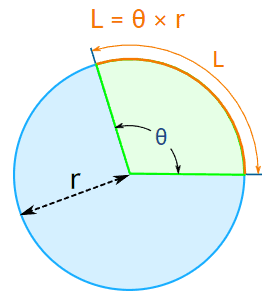
Arc Length
Arc length is the curved distance from one point on the edge of the circle to another point along the circle. This can easily be solved using the formula below. We must know the radius, and angle (θ). This will provide us with the length from one point to the other along the circumference of the circle.
At Online Math Center
Circles are all around us. Understanding the basics of this shape along with the more complex concepts are crucial for every student. At Online Math Center, we ensure that all students leave our school with a deep understanding of circles, including the basics all the way to the arc length. Students can strengthen their skills in foundational topics like this at OMC through our classes and tutoring. With two difficulty levels per grade, OMC works to get every student as advanced as possible; in mathematics and beyond.
Contact us at OMC today to ensure your child gains a concrete, thorough understanding of the most important mathematical concepts like these. Signing them up for classes that are made to fit their specific educational needs will benefit them in the long-term, in mathematics and in daily life.