With all the information passing through our day-to-day channels, we might miss out on the basics. Most mathematical challenges appear when students forget to use basic understandings.
That’s why we have returned with our math symbols series in order to help students and parents navigate through the daily math problems.
Today we are tackling the use of equality, equivalence and similarity in mathematical language. Did you know that less and less people are familiar with standard math symbols such as “approximately”? How often do you see it used in recent years especially with the mass movement to online learning and calculators?
Let’s see how math symbols make our lives easier!
= Equality
One of the most frequently used math symbols, it shows that two values are the same in all aspects. The equal sign is a relation symbol and it is used universally across all languages and cultures.
Usage: A = 5 + 4
B = 4 + 5
Meaning that: A = B
≈ Equivalent
It’s pretty simple to remember what this sign means in mathematical terms. The equivalent sign indicates that two numbers, concepts or ideas are similar under a particular condition. While the equal sign represents the fact that two factors are the same under all conditions, equivalence refers to portions of equality between the two or more factors. Moreover, two factors that are similar under a particular condition, fulfill one of the three equivalence relations:
- Reflexivity: a ~ a
- Symmetry: If a ~ b, then b ~ a
- Transitivity: if a ~ b and b ~ c, then a ~ c
Usage:
Change each of the fractions into equivalent fractions having denominator 24:
- 6/12 = 6×2/12×2 = 12/24
- ³/₈ = …
- ²/₆ = …
- ⁴/₆ = …
We have already mentioned the fact that equivalence indicates a certain similarity.
Then what about the actual similarity concept in mathematical terms? Equivalence has a series of sub-denotations depending on the given variables to values in maths problems.
~ Similarity
Don’t worry if you already feel overwhelmed. The similarity in mathematics is part of the equivalence relations and it is mostly used in geometry and as matrix similarity in algebra. We will deal with similarity in geometry, for now, as this concept in algebra is a bit more complex and usually used in statistics.
Similarity In Geometry
Euclid of Alexandria, the famous Greek mathematician considered the “father of Geometry”, teaches us that two objects are similar if they have the same shape or the same one in reflection.
Therefore, one shape can be obtained from the other by translation, rotation, scaling or reflection. Moreover, when two objects are similar, each is congruent (coinciding exactly when superimposed) to the result of the particular uniform scaling of the other.
Did you also get lost in translation? The figure below will shade some light upon this:

With similar objects, whether you flip them, turn or reflect they keep the same shape and the same size. Here is the trick in solving math problems: when two objects are similar, they have the same angles and the same proportions! Check out the figures below:
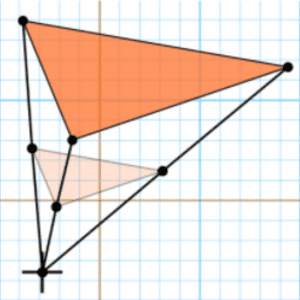
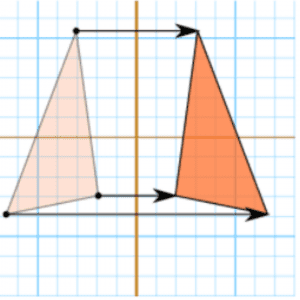
Usage: Calculate the value of t in the following situation:
Condition: Triangle ABC ~ XYZ

Usually, math problems are quite simple once you discover the key which leads to the correct answer. There are tricks and tips that can help you master mathematical problems as long as you understand the language behind symbols.
There are several other symbols related to equivalency that you could stumble upon during mathematical problems, though most of them are used in abstract algebra.
Let’s dive into them!
≈ The symbol for “approximately equal to” or approximated
Usage: A car is sold for $3567. Round the price to the nearest ten (in practice approximation is often used to round up or down prices or numbers, or averages)
≡ It indicates that equality between two factors is true regardless of the given values to the factors (also referred to as identity); used in number theory and modular arithmetic
Usage: (a+b)2 ≡ a2 + 2ab + b2 (in practice, the equal sign is used between the two factors)
≅ It indicates that one mathematical structure is isomorphic to another mathematical structure (operation, relation, metric, or typology); in geometry, it can mean that one shape is congruent to another one.
Usage: The Richter scale, counting numbers by fingers or points given in video games are all basic examples of isomorphic relations.
Do You Want To Learn More About Mathematical Language?
You can get in touch with one of our math tutors or register for one of our math programs where we offer tutoring for children tackling mathematics in middle school or high school.
Online Math Center promotes a learning experience towards excellence and we also offer a tailored tutoring program for academic competitions.