When you decide to participate in a math competition, you should expect your brain to catch fire, especially if on the exam paper, you stumble upon a tricky math problem like the ones below. Most such problems from math competitions are based on logical thinking, so practicing that skill is utterly important. Below, you will find a selection of middle school tricky problems met during math competitions.
Would you solve these math problems?
Logic and Math
The educational platform called Scholastic prides itself on hosting the hardest math challenge. In their past brochures, starting with 2018, you can find samples of their math competitions’ papers. One example is:
When Samantha finally got her phone back, the monkey had drained the battery all the way to 31%, boo! On the bus home, Samantha turned on Top Pop to calm herself. “Too bad your battery’s at 29% now. I’m still at 55%,” Jorge said while watching The Haunted Cave. Samantha eyed their phones thoughtfully. If Jorge’s phone battery drains at the same rate as Samantha’s, and they continue playing their current media, how many minutes will it be before the two phones have the same battery level?
This exercise is rated as Grade 8, so a middle school student at the end of the cycle should be able to solve it. It’s always best to write down the numbers separately so you can understand the relationship between them easier! After you solve the challenge, you can find the detailed solution here.
Number Theory
Considered one of the most challenging math competitions, the International Mathematical Olympiad (IMO) has been busting brains since 1960. In order to see how math challenges have evolved over time, the OMC picked one problem frm 1960s, and one from 2020. Check them below:
2020’s Exam:
For any odd prime p and any integer n, let dp (n) {0,1,…, p – 1} denote the remainder when n is divided by p. We say that {a0, a1,a2, ….} is a p-sequence, if a0 is a positive integer coprime to p, and an+1 = an + dp (an) for n ⩾ 1?
(a) Do there exist infinitely many primes p for which there exist p-sequences {a0, a1,a2, ….} and {b0, b1,b2, ….} such that an ﹥bn for infinitely many n , and bn ﹥ an for infinitely many n?
(b) Do there exist infinitely many primes p for which there exist p-sequences {a0, a1,a2, ….} and {b0, b1,b2, ….} such that ao < b0 but an ﹥bn for all n ⩾ 1 ?
This is a number theory challenge for high school level. Try to solve it and then check your answer here.
The 1960’s Exam:
For what values of the variable x does the following inequality hold:
Logic and Math
The educational platform called Scholastic prides itself on hosting the hardest math challenge. In their past brochures, starting with 2018, you can find samples of their math competitions’ papers. One example is:
When Samantha finally got her phone back, the monkey had drained the battery all the way to 31%, boo! On the bus home, Samantha turned on Top Pop to calm herself. “Too bad your battery’s at 29% now. I’m still at 55%,” Jorge said while watching The Haunted Cave. Samantha eyed their phones thoughtfully. If Jorge’s phone battery drains at the same rate as Samantha’s, and they continue playing their current media, how many minutes will it be before the two phones have the same battery level?
This exercise is rated as Grade 8, so a middle school student at the end of the cycle should be able to solve it. It’s always best to write down the numbers separately so you can understand the relationship between them easier! After you solve the challenge, you can find the detailed solution here.
Number Theory
Considered one of the most challenging math competitions, the International Mathematical Olympiad (IMO) has been busting brains since 1960. In order to see how math challenges have evolved over time, the OMC picked one problem frm 1960s, and one from 2020. Check them below:
2020’s Exam:
For any odd prime p and any integer n, let dp (n) {0,1,…, p – 1} denote the remainder when n is divided by p. We say that {a0, a1,a2, ….} is a p-sequence, if a0 is a positive integer coprime to p, and an+1 = an + dp (an) for n ⩾ 1?
(a) Do there exist infinitely many primes p for which there exist p-sequences {a0, a1,a2, ….} and {b0, b1,b2, ….} such that an ﹥bn for infinitely many n , and bn ﹥ an for infinitely many n?
(b) Do there exist infinitely many primes p for which there exist p-sequences {a0, a1,a2, ….} and {b0, b1,b2, ….} such that ao < b0 but an ﹥bn for all n ⩾ 1 ?
This is a number theory challenge for high school level. Try to solve it and then check your answer here.
The 1960’s Exam:
For what values of the variable x does the following inequality hold:
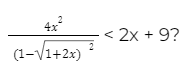
You can check the rest of the math exercises on the 1960’s math competition here.
Try to solve the tricky math problems above, and then…
Hop on the math tutoring programs that the Online Math Center offers to middle or high school students. Our math tutors tackle diverse math challenges, including special tutoring for nailing math competitions. Have questions?
Contact us to discuss our math learning philosophy and how we can help you put with mathematics.