When we hear the word transformation, we may think of a home makeover, a metamorphosis, or maybe even a famous movie about robots. It’s easy to forget that transformations have a place in the world of mathematics, too. In geometry, transformations are changes in the appearance of a two-dimensional figure. This could mean a rotation, reflection, dilation, or translation. In every transformation, there is a pre-image and an image. The pre-image is the object before the transformation, and the image is the object after the transformation has been applied.
Before we dive into transformations, we need to briefly discuss an important topic: isometry. At its core, an isometry is a rigid transformation that does not change the size or shape of an image. See if you can identify which of the four transformations below are isometric, and we’ll reveal the answer at the end. Let’s dive right in!
Rotation
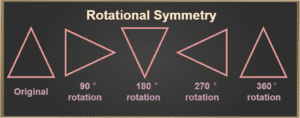
Rotations are easy to recognize in the real world. We see them every day, from rotating tires to rotating a couch, to activities such as crop rotation. In geometry, rotation is essentially the same, it is the act of turning around a defined axis or center. This means determining the axis or center and turning the object by a certain degree in a specific direction. The object can be rotated clockwise (to the right) or counterclockwise (to the left).
A full rotation has 360° degrees, meaning that rotating an object halfway would be 180° and, therefore, rotating an object one-quarter of the way would be 90°. In the example below, the axis is the center of the triangle and you can see some of the different degrees of rotation possible. It is important to note that it is entirely possible to rotate an object to a seemingly random degree, such as 83° degrees, but this is not commonly found in word problems or real-life situations.
Reflection
Another transformation of note is a reflection. This is where an object is flipped to create a congruent mirror image of itself. We quite literally see our own reflection every day (or multiple times a day) in a mirror. The object is flipped over a line (either imaginary or drawn) typically on a coordinate plane. However, it is not just flipped to any location on the other side of the line. It is equidistant, meaning that both reflections are the same distance from the line. Every vertex (or corner) of that object is equally as distant from the mirror line as the object on the other side.
Dilation
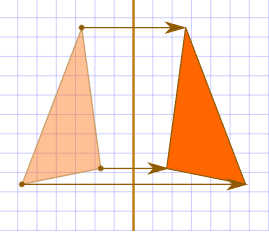
Dilation is also known as resizing: adjusting the object’s size without changing the shape. When we go to the eye doctor, we may have our eyes dilated which essentially means our pupils are increased in size, but not in shape. We apply this to geometry when stretching or shrinking shapes, most commonly on a coordinate plane. With dilation, the pre-image and image are not congruent, but they are similar. They are similar because the shape is the same, but the size of the shape has changed. Two shapes can only be congruent if the size has not changed. As you can see below, the pre-image is the original object, but when resized it grows larger and becomes the image.

Translation
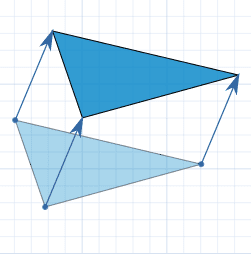
The act of simply moving or sliding an object in geometry is called translation. In a geometric translation, the size, shape, and orientation all remain the same. Each point of the object is moved the same distance in the same direction. The pre-image and image remain congruent as their size and shape have not changed, simply the location. In the example below, you can see the light blue triangle representing the pre-image, and the darker blue triangle as the image.
Isometry
Earlier in this article, we touched on isometry and its definition: a rigid transformation that changes the shape but not the size of an object. Only 3 of the 4 transformations are isometric: rotation, reflection, and translation. This is because the final image in all four transformations is congruent to the pre-image. However, in a dilation, we now know that the pre-image and image are not congruent because the size of the object has changed.
At OMC
Transformations in geometry are important not only to grasp the topic of geometry inside the classroom better but also to help young students understand and apply these concepts in their daily lives. At Online Math Center, we ensure that all students leave our school with a deep understanding of relevant geometry concepts such as reflection, dilation, transformation, and translation. Whether it comes easily to a student or not, we offer classes and tutoring that will assist them in strengthening their foundation in mathematics. OMC works to ensure that every student reaches or surpasses their full potential in math class and beyond.
Contact OMC today to help ensure your child gains a solid, complete understanding of the most important mathematical concepts, like geometric translations, by signing them up for classes that are tailored to their specific educational needs.