Young math students learn a lot about lines, angles, and other shapes when they’re studying math in middle school. Before they can find the volume of a cone or the area of a circle, they must learn everything there is to know about the humble line. Understanding the basics can help ensure that students become comfortable with math from an early age and, in the long run, can reduce their anxiety around the subject.

Whether they are parallel or perpendicular, we will talk about how different types of lines interact with each other and look at what we can learn by properly understanding these lines. 

What Are Parallel Lines and Perpendicular Lines?

Parallel and perpendicular lines are the two most common sets of lines that young math students are going to deal with in 6th grade. While many students often get confused between the two, there are easy ways to remember which is which.

We can say that two lines are parallel if they are the same distance apart at every point. Essentially, parallel lines will never meet. They will always be the same distance apart and they will never intersect.

On the other hand, lines are considered perpendicular if they are at a right angle to one another. 

So, what’s the difference between a parallel line and a perpendicular line? 90°…

Apologies for the terrible joke, but it does raise an important piece of information. We need to pay attention to the relationship between certain types of lines and angles. 

 

Pairs of Angles

Imagine, for one moment, that we have a pair of parallel lines. Now, imagine this pair of parallel lines getting crossed by another line. We call this 3rd line a transversal. 

Transversals tell us much about the angles they create when they cross parallel lines. They create what we call pairs of angles. These pairs of angles can be used to test if two lines are really parallel.

For example, a straight line is 180°. This tells us that if we have a straight line that gets cut by a transversal, the two angles the transversal creates will add up to 180°.

Similarly, we can use our knowledge of angles to determine if the lines we are dealing with are, in fact, parallel. Here are some examples (and an accompanying diagram) featuring some of the special pairs of angles that students will come to understand in 6th grade:

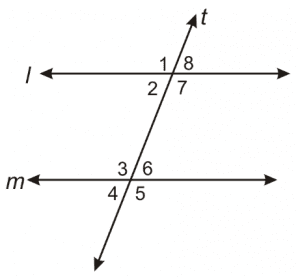
If any pair of … Example from diagram:

   

Corresponding angles are equal 1 = 3

or  

Alternate interior angles are equal 2 = 6

or  

Alternate exterior angles are equal 8 = 4

or  

Consecutive interior angles add up to 180° 7 + 6 = 180°

   

… then the lines are Parallel!

Slope

You’ve seen ways in which we can use angles to verify if lines are parallel. Another way we can identify a pair of parallel lines is by looking at their respective slopes. But what is the slope and why is it important in algebra class?

 

The slope of a line shows us how steep a line is, provided that line is straight. If lines are parallel, their slopes will be equal.

 

Now that we know what the slope of a line is, we need to figure out how we calculate it. In essence, the slope of a line measures the change in height and the change in horizontal distance.

 

Therefore, we can say that slope = Change in Y divided by the change in X.  

 

We write the equation for slope in the following form: y = mx + b

 

In this equation, y is the m is the slope, while y and x represent the points along their respective axes (x is the horizontal axis, while y is the vertical axis).

 

To find the slope of a perpendicular line, we simply need to know the slope of the line to which it is perpendicular. The perpendicular line will be a value of -1/m where m is the slope of the other line.

 

For example: if our line has a slope of 4, a perpendicular line will have a slope of -¼.

 

To make sure you’re working accurately, multiply the two slopes together and, if your calculations are correct, you will get -1.

 

This is just the tip of the iceberg in terms of the interesting insights we can draw from parallel and perpendicular lines and the corresponding angles. Be sure to check back for more blog articles on this topic in the near future.

OMC 6th Grade Math Courses

At OMC, we fully understand the importance of a good math foundation. The reality is that some kids excel, while others struggle in math class. Some have massive gaps in their knowledge, others are looking for additional, more challenging work to continue growing as a student and mathematicians.

 

To make sure we can help each math student who needs us, we offer individual lessons, dedicated 6th grade math lessons, and special classes to prepare for examinations or get ready to enter math competitions.

 

Contact OMC today to get your child on the path toward mathematical excellence!