Do you know what’s the next simplest geometrical figure after the point? It’s a straight, infinite geometrical figure. It’s the line! Compared to the point which has no dimensions, the line is one-dimensional.
What is the use of the line in geometry?
When a line has two ends it is called a line segment or side-line and we usually use line segments to name the sides of the triangle. When a line has just one end, it is called a “ray”.
Lines are part of any geometrical shape and plane, that’s why it is important to know the basics about lines.
Math Symbols Related To The Line
“ ↔ “ – this symbol represents the infinite line; usually is noted above two letters to symbolize that the line on which the two points are, is an infinite line, example:
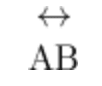
“ ⎻ “ – a simple line above two letters indicates a line segment, which starts at point A and ends at point B:
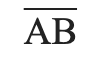
“→” – this symbol indicates a ray, which starts from point A;
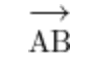
“∠” – this symbol indicates an angle formed by two rays, example: ∠ABC = 30°
“⟂” – this symbol indicates that two lines are perpendicular, thus forming a 90° angle. The notation would look like this:
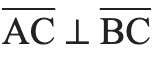
“ ∥ “ – this symbol indicates that two lines are parallel to each other:

When two lines are not parallel, we would use the “∦” symbol. When two lines are parallel and equal, we use the symbol “⋕” .
Types of Lines
In geometry, there are a variety of lines that relate to spatial relationships between points or angles. It’s pretty simple to memorize the type of each line, so here we go:
Vertical line
A vertical line is a straight line that goes from top to bottom.
Horizontal line
A horizontal line is a straight line that goes from left to right.

Parallel lines
Two or more lines that do not intersect at any point, infinitely, are called parallel lines.

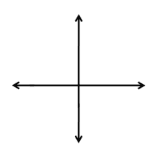
Perpendicular lines
Two straight lines that meet at an intersection point and form a right angle (90°) are called perpendicular lines.
Oblique lines
These lines are diagonal or slanting lines.
Diagonal or oblique lines can be perpendicular or parallel.
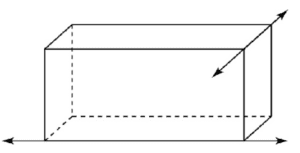
Skew Lines
When it comes to spatial geometry, two non-parallel lines that are not intersecting in a given space are called skew lines.
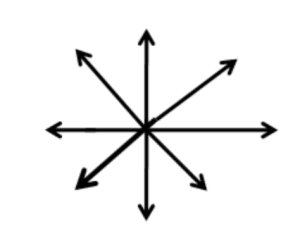
Concurrent lines
In our past article, we mentioned concurrency in points. Since two or more lines can cross through a common concurrent point, these lines are also called concurrent.
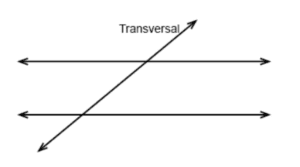
Transversal lines
The line that cuts two or more straight lines is called a transversal line. The cut lines are not necessarily parallel.
Coplanar lines
Coplanar lines are straight lines that exist in the same spatial plane.
The Rules Of Lines In Math
- Alternate angles are equal.
- Corresponding angles are equal.
3. When 2 straight lines intersect, they form vertically opposite and equal angles.
Remember the above simple and short line rules and get ready to apply them in daily life. Did you know that line calculations are an important part of computer graphics and architecture?Let’s PRACTICE!
Solve the following exercises:
#1. Look at the image below and choose which option is true.
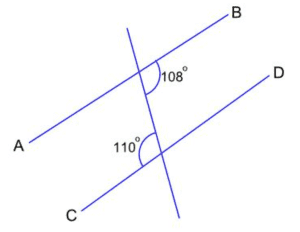
2. are not parallel because the two given corresponding angles are not equal
3. are parallel lines
4. are not parallel because the two given alternate angles are not equal
5. are not parallel because the two given consecutive interior angles do not add to 180°
#2. Look at the image below and choose which option is true.
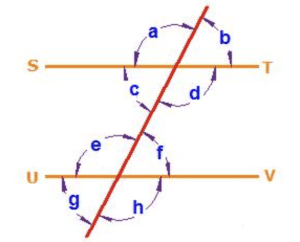
1. consecutive interior angles
2. corresponding angles
3. alternate interior angles
4. vertical angles
#3. Check out the image below:
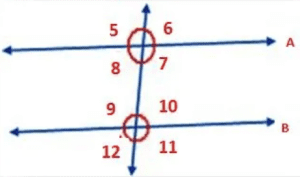
#4. Check out the image below and then choose the correct option from the statements below:
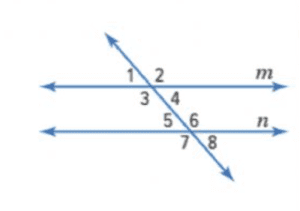
1. Angles 2 and 6 are examples of vertical / corresponding angles.
2. Angles 1 and 8 are examples of alternate interior / exterior angles.
3. The angle that is corresponding to angle 8 is angle 3 / 4.
4. If lines m and n are parallel, then angles 3 and 6 / 8 have equal measures.
If you want to memorize the types of lines better, you can always solve some online exercises, here.When it comes to solving geometry problems, practice does indeed help you become better at mathematics.
For more fun exercises on lines, you can check out these questions. Additionally, if you want to learn more about 4th-grade mathematics, our OMC tutors offer individual and group lessons that turn any student into a math champion!
Reach out to us and meet our OMC math tutors!